La regresión logística y el cálculo de porcentajes apostados

 Esta entrada voy a dedicarla a la regresión logística, aplicada al cálculo de porcentajes apostados el mismo día de sellado.

Es necesario darle una máxima importancia a unos porcentajes apostados a cierre de calidad. De ellos depende calcular correctamente qué signos son rentables y cuánto lo son, llevando nuestra jugada a un término u otro en función de su relación con los datos reales. Los porcentajes reales en cambio son bastante más estables, y no supone un problema actualizarlos el día que vayamos a validar las apuestas dada la amplia información disponible al segundo por las casas de apuestas.

SELAE tan sólo publica los porcentajes del día anterior, y es sabido que la mayoría de las apuestas se sellan el mismo día del cierre. Esto supone un problema, ya que el tipo de apostante que sella días antes, no es el mismo que sella horas antes de que se dé por comenzada la jornada. En esta categoría entran peñas grandes, medianas y pequeñas con sistemas basados en la rentabilidad que modifican notablemente los porcentajes apostados.

Necesitamos por tanto una muestra más o menos estable de perfiles de jugadores diversos actualizados el mismo día. Afortunadamente, la página web de Eduardo Losilla (antes Quinielista.com), nos sirve una muestra actualizada permanentemente hasta la hora de cierre. Sin embargo, como digo, se trata de una muestra distinta de la que compone el conjunto de apostantes de LAE, siendo la composición de peñas y particulares distinta. Necesitamos relacionar los porcentajes finales de LAE con la composición que nos da dicha web. Esto se hace con una regresión, concretamente la logística, que nos ofrece una enorme flexibilidad, y la posibilidad de relacionar varias variables con una sola (los apostados finales).

Mi fuente principal de conocimiento y mi referencia principal en materia de matemáticas, y puede resultar algo triste decirlo, es la Wikipedia. También echo mano de otras fuentes, pero la de origen suele ser esta misma. Sin enredarme a dar explicaciones más profundas, y dando la referencia de esta enciclopedia digital (que recomeindo consultar para este término), paso a explicar someramente la regresión logística.

Esta regresión se basa en la función sigmoidal. Dicha función, y la regresión en sí, son utilizadas en los algoritmos de redes neuronales. Tal vez un día me anime a publicar una entrada complementaria acerca de este tema, pero por el momento el único objetivo será la regresión.

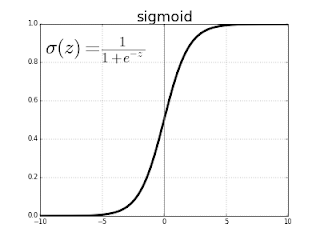
El aspecto de la función sigmoidal, tiene una pinta tal que así:

He tomado una imagen de la web (espero que no se queje nadie) que la representa. Incluso incuye una fórmula que debo matizar y completar:

$$p_i = \frac{1}{1 + e^{-(\beta_0 + \beta_1 x_{1,i} + ... + \beta_k x_{k,i})}}$$

La duda puede surgir por el exponente del número e. En realidad no es más que la ecuación de una aplicación linal con k variables independientes, multiplicada cada una por un coeficiente beta. Cada variable independiente, será una entrada de datos para calcular la regresión, y en principio podemos tener tantas variables o entradas como queramos.

Otro elemento imprescindible para realizar la regresión es la función logit:

$$ln \frac{\pi (x)}{1 - \pi (x)}$$

Con todo esto, y si es necesario (que lo será), echando un ojo a la entrada de la Wikipedia, podemos resolver la regresión. Para ello, he crado una hoja de Google Sheets en la que desarrollo todo el cálculo. En esta ocasión, como en la pasada entrada, no voy a emplear ninguna macro ni código JS, todo lo necesario nos lo ofrecen las hojas de cálculo, ya sean de Google o del propio Office de Microsoft (de hecho las funciones empleadas llevan el mismo nombre en ambas plataformas).

https://docs.google.com/spreadsheets/d/1cqujfD2f3APY_Zw2pAj8Z_MyPRMdwwU6XimtKiSRyDE/edit?usp=sharing

El anterior enlace da acceso de lectura a la hoja que he preparado para ilustrar el cálculo. Resulta imprescindible sacar una copia al Drive personal de cada cual para poder manipularla, actualizarla con nuestros propios datos, etc.

Como se trata de un mero ejemplo, tan sólo he introducido dos variables, el porcentaje real, y los apostados (de cierre) de la página web de Eduardo Losilla, llamados allí %Quinielista o simplemente QUI. El que desee profundizar en unos apostados estimados más parecidos de los que obtendremos tal vez le interese hacer algún estudio personal de evolución semanal. Esto obviamente requiere recopilar datos durante largos periodos y ser bastante meticuloso. Yo en este ejemplo, tan sólo me he limitado a descargarme el histórico de cierre disponible en la API de Losilla, que además es accesible a todo el mundo.

En primer lugar es necesario preparar los datos para realizar la regresión. Lo primero que debemos hacer es pasar los porcentajes que se encuentran en tanto por cien a tanto por uno, especialmente los de la variable dependiente que serán los LAE finales. Repito, imprescindible disponer de los datos de la variable dependiente en tanto por uno, esto debe ser así para poder emplear correctamente la función logit representada anteriormente.

En la función logit presentada, los pi(x) tan sólo se refieren al porcentaje de probabilidad de la variable dependiente. En la Wikipedia se puede ver el desarrollo de la formulación original, y cómo se relaciona la logit con la función del exponente del número e de la primera fórmula. Aquí partimos de unos pi(x) conocidos, pero para el que quiera dar con la metodología de las redes neuronales, que no se le escape que la cifra de la variable dependiente no la tendrá, debiendo realizar una ordenación de los datos, y asignar a otra variable de apoyo dos únicos valores (0 y 1, acertado y fallado).

En la hoja "Organizacion" he dispuesto las columnas de modo que pueda aplicar la función "ESTIMACION.LINEAL" de la hoja de cálculo. Las dos variables independientes deben estar en columnas contíguas. También una tercera columna en la que he aplicado la función logit a la variable dependiente. El que tenga dudas de cómo se ha calculado la logit, puede inspeccionar la fórmula de la columna de LAE en la citada hoja.

Lo que se realiza a continuación es la obtención de los coeficientes beta de la función exponente del número e. Para ello basta aplicar la función "ESTIMACION.LINEAL" presente en la hoja de coeficientes. Por comodidad de representación de los datos, he agrupado los datos según 1X2, aunque se podría obtener un único conjunto de coeficientes reposicionando todos los datos independientemente del 1X2, obteniendo una única regresión. Así pues, tendremos tres regresiones, una por signo. La función "ESTIMACION.LINEAL" detecta dos columnas como "conocido x" dando lugar a una regresión lineal múltiple (de dos variables, reales y porcentajes del quinielista). Si no se ha entendido algo se puede inspecionar la fómula de la hoja, y buscar información acerca de la misma.

Con lo anterior, habremos obtenido dos coeficientes (beta sub1 y beta sub 2, uno por variable) y una constante (beta sub 0). Pues entonces eso es todo, ya tenemos todo lo necesario para estimar los apostados finales a partir de los reales y los QUI de las horas antes del cierre de apuestas. En la hoja "Validacion" sólo nos queda aplicar la primera fórmula con nuestros coeficientes beta y los datos de que disponemos, ajustamos los tres porcentajes al 100% y vemos en la comparación que he dispuesto en la hoja cuánto se desvían de los finales que en realidad se dieron cada jornada.

Espero que la entrada haya sido de utilidad, y que de cada uno surja la curiosidad de introducir otras variables adicionales, o incluso aplicar la regresión logística a otros campos como pudiera ser el cálculo de nuestros reales personales a partir de, por ejemplo, estadísticas de equipo.

Un saludo a todos, y suerte.