Periodos de maduración de la jugada

 Después de varias semanas sin publicar nada, vengo a escribir esta entrada acerca de un tema que he estado estudiando en los últimos días. Se trata del tiempo necesario, o más concretamente jornadas de simulación, en que se dará un recuperación superior al 100% de lo invertido hasta la fecha. Es un tema importante, ya que nos dirá cómo de viejos nos haremos hasta lograr obtener beneficios de nuestra jugada.

Cierto es que cada jornada es distinta, y que las simulaciones las haremos sobre unos mismos datos (los de la propia jornada a jugar), pero si mantenemos las estadísticas de las simulaciones jornada tras jornada, lograremos también que los datos se cumplan en un tiempo determinado, normalmente en función del tamaño de apuesta. Es obvio que no tardaremos lo mismo en superar la frontera de la rentabilidad con 300 columnas, que con 10.000. Los tiempos son muy distintos y es el gran hándicap de las peñas pequeñas como la mía.

En primer lugar voy a compartir la aplicación web que ya había compartido en anteriores posts con alguna pequeña modificación:

https://drive.google.com/file/d/1ZkvxcVMRgMoMaYdFj_0OMmKLTqZ0up8L/view?usp=sharing

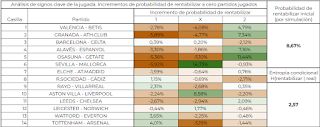
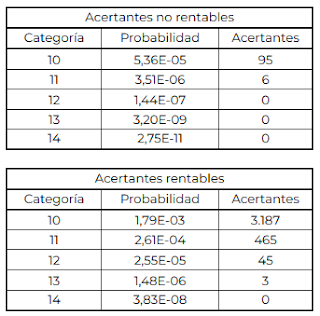
En el anterior enlace se puede descargar esta app. Como ya expliqué, se trata de un código JS muy sencillo, y sin apenas capa de presentación para evitar complicarlo más de lo debido. Los cambios que he introducido consisten en una barra de progreso (por temas de usabilidad), y en dos tablas donde presento los datos que anteriormente eran referidos tan sólo al conjunto de premios que ahora he ampliado a cada categoría. Con esos datos, además de conocer los retornos y esperanza matemática de la jugada, podrá conocerse también la específica para cada categoría. La segunda tabla es referida a los datos puros y duros de la simulación por premios, y presenta el número de premios obtenido y la cantidad en euros acumulada a lo largo de las simulaciones.

Con la segunda tabla (la inferior), también podemos obtener los datos de EM y premios medios. Basta con operar de manera sencilla dividiendo el acumulado en euros por el número de premios, para obtener el premio medio de cada categoría, y relacionar el importe acumulado dividiéndolo por el importe jugado a lo largo de las X simulaciones, para saber la esperanza matemática exacta, bien de la jugada o de cada categoría.

Pero lo anterior no es el tema que me ocupa en este post. Como dije, el objetivo es conocer los periodos de maduración de la jugada en concreto. Para ello trabajaremos sobre un libro de cálculo de Google que también había presentado anteriormente:

https://docs.google.com/spreadsheets/d/1yRe2EssWbokajM1f8zTLW_qr9cnMvpMruY8v-ohNFz0/edit?usp=sharing

En esta versión de nuestro libro de Google, he introducido una nueva hoja dedicada a la maduración, y he cambiado la casilla que antes era del 55% de la recaudación, haciendo que se refiera al máximo importe obtenido en una simulación del conjunto de simulaciones. Ese 55% se utilizaba para la integación de la curva loglogística y ahora también, tan sólo se cambia el límite de la integral definida. Ese dato lo obtendremos de la tabla que aparece en la aplicación web. Otro cambio en el libro, es el modo en que se lanza el dado loglogística. De modo que si genera un importe superior al máximo lo desecha, y continúa hasta que encuentra uno dentro de los límites.

Vamos al lío... En la hoja 'Maduracion' del libro veremos varios datos presentados de manera tabular. En las dos primeras columnas he establecido un periodo de 25 años, año a año, y el número de jugadas realizadas suponiendo un total de 60 jornadas anuales. En las siguientes columnas, recurro a una función que ya había programado y presentado en anteriores posts. Se trata de la simulación con un dado de premios de la jugada (hallados los parámetros alfa y beta de la distribución loglogística de la jugada), y que utilizo para hallar a su vez los parámetros de un ajuste normal a un conjunto de varios periodos (los de las columnas más a la izquierda). A partir de ahí, hallada la media y la desviación de la lognormal, basta usar los percentiles de la jugada en una función por defecto de Google y también presente en Excel (DISTR.LOG.INV). Esta función nos permite introdicir un percentil, la media y la desviación, y obtener el valor de la variable, que es el importe en euros estimado de premios. Si le restamos además lo jugado hasta ese punto, tendremos nuestro bankroll en ese instante.

Si hasta aquí existen dudas, que seguro que las habrá, sugiero repasar anteriores entradas y revisar el contenido de las celdas del libro, intentando comprender el desarrollo del cálculo en el mismo.

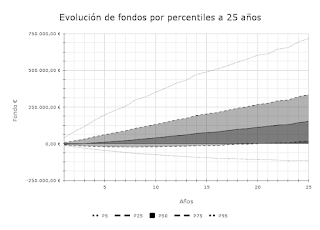
Para las series anteriores, he establecido los percentiles 5, 25, 50, 75 y 95, que representan el rango intercuartil y el intervalo de un 90% de confianza para el desarrollo temporal de la jugada, y que he plasmado en un gráfico presentado en la hoja 'Panel':

En esta imagen se pueden ver los datos tabulados. Podríamos proceder de manera distinta, usando el dado de la loglogística para crear series de líneas que recrearían aleatoriamente la evolución de varias simulaciones a lo largo del tiempo, con lo que tendríamos una nube de líneas de la que intuiríamos estos mismos rangos de confianza, pero Google Sheets tiene un problema de limitación de número de columnas y filas que nos podrían complicar representar tantos datos.

El anterior gráfico nos muestra las posibles evoluciones de la jugada en las simulaciones, pero nos queda conocer los tiempos exactos de maduración. Para ello, en la columna 'K' de la hoja 'Maduración', he empleado la función por defecto DISTR.LOG.NORM, para un valor de la variable igual a lo que se habría jugado en cada instante. Así tendríamos la probabilidad de obtener la neutralidad de la jugada para cada periodo. Esta columna es necesario relacionarla con el número de jornadas. Probé con varias distribuciones que me permitiesen linealizar el problema, y que me permitiese hallar fácilmente los parámetros de la distribución que relaciona ambas variables. Probé con la Weibull, Gumbel, Exponencial... Pero la que las relaciona a la perfección es la Exponential Power Distribution (Smith y Bain, 1975). No me atrevería a dar una traducción exacta porque no encontré literatura en castellano en la web que la mencionase, pero lo que nos interesa es la ley en concreto, que se expresa de la siguiente forma:

$$exp(1-e^{(\lambda x)^{\alpha}})=p$$

Donde la 'p' es la probabilidad acumulada que hemos calculado. Si aplicamos por dos veces el logaritmo a ambos lados de la ecuación nos queda:

$$Ln[Ln(1-Ln(x))] = \alpha Ln(\lambda) + \alpha Ln(x)$$

Y que traducido a la ecuación de la recta:

$$y = mx + b$$

Donde:

$$b = \alpha Ln(\lambda)$$

$$m = \alpha$$

$$x' = Ln(x)$$

$$y = Ln[Ln(1-Ln(x))]$$

Así pues preparamos la variable X y nuestra Y como se muestra en las anteriores fórmulas en las columnas correspondientes de la hoja 'Maduración', y hallamos la ecuación de la recta. Para no ejercer un acto de fe, en el siguiente grafíco que adjunto en la hoja, se muestra el ajuste de la recta al preparar los datos (además también podemos ver el coeficiente de correlación):

Como se puede observar la correlación es casi perfecta.

Con las ecuaciones de arriba y la regresión, ya podemos calcular nuestro alfa y nuestro lambda para la distribución. En la hoja 'Panel' presento el valor de los coeficientes, y además dos valores que considero de interés, que son la mediana y la media. En el caso de la mediana he despejado la X de la ecuación desarrollada de la recta presentada anteriormente: 

$$x = exp((Ln[Ln(1-Ln(x))] - \alpha Ln(\lambda)) / \alpha )$$

Esta ecuación es de especial importancia, pq es un generador de números aleatorios según la distribución que estamos tratando. Así con un random de programación, podemos obtener número de jornadas en las que rentabilizaremos de manera aleatoria, u obtener la propia mediana sustituyendo la 'p' por el valor 0'5. 

La media por su parte es algo más complicada de obtener. Al no encontrar fórmula específica de la media para este tipo de distribución, lo que he hecho ha sido crear un segundo dado similar al de la loglogística, pero para esta distribución. El código lo muestro aquí, aunque puede inspeccionarse en el apartado 'Herramientas' -> 'Editor de secuancias de comandos':

function media_EPD(alfa, lambda, simulaciones) {
  var acum = 0.0;
  for(var i = 0; i < simulaciones; i++) {
    acum += dado_EPD(alfa, lambda);
  }
  return acum / simulaciones;
}

function dado_EPD(alfa, lambda) {
  var r = Math.random();
  var sim = Math.exp((Math.log(Math.log(1 - Math.log(r))) - alfa * Math.log(lambda)) / alfa);
  return sim;
}

Sencillo.

La intepretación que podemos darle a la mediana es el número de jornada en que el 50% de las veces estaremos en beneficios, y el otro 50% en pérdidas, mientras que la media considera las simulaciones en que cruzaremos la línea de la rentabilidad, considerando incluso las más desfavorables (casos extremos en que nos mantendremos en pérdidas durante largos periodos de tiempo). 

Os dejo hasta la próxima entrada, que no estoy seguro de cuándo será. Todo depende de si encuentro algo interesante que añadir por aquí. Cualquier duda, me encontraréis en redes, comentarios al post, o email. Un saludo.