Herramienta EM
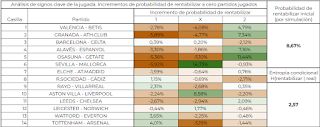
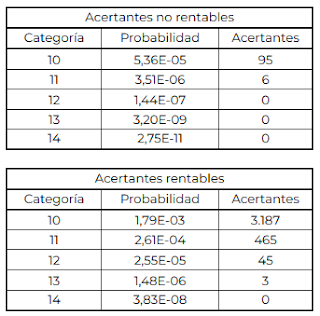
En esta entrada voy a compartir una herramienta programada en Java para filtrar las columnas de nuestra madre por las EM de todas las categorías de 10 a 14. Antes de nada comentar que no debe usarse para filtrar las 4'7 millones de columnas, ya no por el tiempo requerido, que sería excesivo, si no porque también puede ralentizarse a medida que avance y/o dar un error de memoria. El algoritmo realiza una memorización de premios de columnas ya calculadas para acelerar el proceso, de hecho observaremos que al filtrar nuestra madre irá cogiendo velocidad al no necesitar de algunos nuevos cálculos. También me han avisado de que otras herramientas para calcular las EM no coinciden con mis cálculos, y que ni siquiera coinciden entre ellas, por lo que me surge cierta duda acerca de la fórmula y algoritmo empleados. Como es algo mío, y que he repasado a conciencia, voy a presumir de que mi algoritmo es el correcto, aunque de momento no pueda garantizarlo al 100%. Las herramientas que me han...